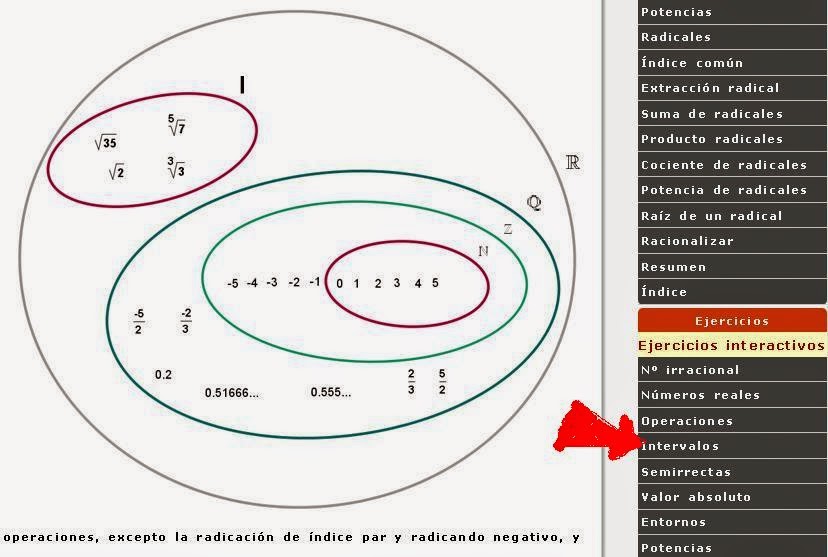
En matemáticas, los números reales (designados por
\mathbb{R}) incluyen tanto a los números racionales (positivos, negativos y el
cero) como a los números irracionales; y en otro enfoque, trascendentes y
algebraicos. Los irracionales y los trascendentes1 (1970) no se pueden expresar
mediante una fracción de dos enteros con denominador no nulo; tienen infinitas
cifras decimales aperiódicas, tales como: \sqrt{5}, \pi, el número real log2,
cuya trascendencia fue mentada por Euler en el siglo XVIII.
Los números reales pueden ser descritos y construidos de
varias formas, algunas simples aunque carentes del rigor necesario para los
propósitos formales de matemáticas y otras más complejas pero con el rigor
necesario para el trabajo matemático formal.
Durante los siglos XVI y XVII el cálculo avanzó mucho aunque
carecía de una base rigurosa, puesto que en el momento no se consideraba
necesario el formalismo de la actualidad, y se usaban expresiones como
«pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una
serie de paradojas y problemas lógicos que hicieron evidente la necesidad de
crear una base rigurosa para la matemática, la cual consistió de definiciones
formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.
En una sección posterior se describirán dos de las definiciones precisas más
usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números
racionales y cortaduras de Dedekind. (http://es.wikipedia.org/wiki/N%C3%BAmero_real)





No hay comentarios:
Publicar un comentario